Functional-Light JavaScript - Pure Function

前言

此為 frontend master 的 Functional-Light JavaScript, v3 的課程筆記，這篇主要講的是 pure function，內容不完全和課程編排相同，單純是個人消化過後的編排。

因為剛開始學 functional programming 的緣故，內容、觀念可能會有諸多錯誤，如有發現錯誤麻煩不吝指教，感謝！

Function Purity

最一開始要先談 pure function 是因為 pure function 是 functional programming 的基石，如果缺少了 pure function，那使用 functional programming 的好處可以說是少了很多。

一般來說，如果我們下了 pure function 這個關鍵字去 google，會在大多數的文章看到 pure function 會符合以下的定義：

1. same input, same output
2. no side-effects

(圖片取自 What Is a Pure Function in JavaScript?)

所以我們就要逐條來討論這兩個定義是什麼意思，以及除了這兩個定義以外，有沒有什麼可以補充的內容。

Function vs Procedure

在談 pure function 的上述兩個定義以前，不如先來聊聊在 FP 中，什麼叫做一個 function。

function 在 FP 的定義上來說，就是它必須要有 input，也必須要有 output，所以如果你寫的 function 長得像這樣：

function addNumbers(x = 0, y = 0, z = 0) {
  const total = x + y + z
  console.log(total)
}

function extra(x = 10, ...args) {
  return addNumbers(x, 40, ...args)
}

addNumbers 就不是一個 function，因為它只有 input，沒有 output，這個會被叫做 procedure，指的是一段邏輯的集合。

那另一個有趣的問題是 extra 算是 function 嗎？也不算，因為 function 只會 call 其他 function，如果用到 procedure 就不算 function 了。

所以在最初始的 function 定義來說，我們「必須要有 input，也必須要有 output」，不過這仍然不夠完整，因此我們繼續往下探討。

Function Naming Semantics

看到上面這個圖形很懷念對吧！這是我們國中時期的數學，在談論這個函數的時候，我們會將 x 代入 0，得到 3；代入 1，得到 5 之類的，這樣依此類推代入各種數字，將結果點在圖形上，最後把所有點點連起來就得到上面的圖形。

這段數學函數跟程式碼的表達方式很像：

// f(x) = 2X ^ 2 + 3
function f(x) {
  return 2 * Math.pow(x, 2) + 3
}

從上面這段程式碼來思考，x 和 y 是有一定的關聯性的，比如我 x 放進 2，那 y ，也就是 f(x) 就會是 11；如果 x 放進 3，那 y 就會是 21，當 x 是某個數字的時候就會透過它來計算，得到相對應的 y。

Kyle Simpson 是如此說的：

Function: the semantic relationship between input and computed output

也就是 function 的 input 和 output 是會有一定的語意關聯性的。

不過這段定義也還不夠完整，讓我們繼續看下去。

Side Effects

side effects 的定義

講到副作用，讓我們先查查維基百科，維基百科對於 副作用 的定義是這樣的：

在電腦科學中，函數副作用指當調用函數時，除了回傳函數值之外，還對主調用函數產生附加的影響。例如修改全域變數（函數外的變數），修改參數或改變外部存儲。

如果一個函數通過隱式（英語：Implicit）方式，從外界獲取資料，或者向外部輸出資料，那麼，該函數就不是純函數，叫作非純函數（英語：Impure Function）。

隱式的意思是，函數通過參數和回傳值以外的渠道，和外界進行資料交換。比如，讀取全域變數，修改全域變數，都叫作以隱式的方式和外界進行資料交換；比如，利用 I/O API（輸入輸出系統函式庫）讀取設定文件，或者輸出到文件，列印到螢幕，都叫做隱式的方式和外界進行資料交換。

簡而言之，就是 function 本身不是獨立的，它和外界產生了聯繫，像是讀取到外部的 variables、修改外部的 variables，都會產生 side effect，舉例來說：

function shippingRate() {
  rate = ((size + 1) * weight) + speed 
}

let rate;
let size = 12
let weight = 4;
let speed = 5;
shippingRate();
console.log(rate) // 57

size = 8
speed = 6
shippingRate();
console.log(rate) // 42

很明顯的，shippingRate 就和外部的 variables 產生關聯了，因為它用到了外部的 variables 進行某些計算了對吧。

那如果我們把程式碼改成這樣：

function shippingRate(size, weight, speed) {
  return ((size + 1) * weight) + speed 
}

let rate;
rate = shippingRate(1, 2, 3) // 7

就沒有 side effect 了，我們單純依賴 function 自身的 input 進行計算，得到 output 並 return，也就是說 function 是一個獨立的存在。

⚠️ 在課程裡 Kyle Simpson 說這不只是有沒有使用到外面的 variable 這樣而已，而是「pure function need direct inputs and direct outputs」

我對這段話的理解是指 function 會直接地使用 input 進行計算得到 output，比如上面的 shippingRate 直接拿 size, weight, speed 三個 input 計算出了 output。

因為我對於他提出的「direct」理解還不夠深入，怕造成誤會就先省略了這個定義。

例外 - Closure

關於「不依賴到外部的變數」這個定義有個例外，那就是 Closure 的狀況：

function addAnother(z) {
  return addTwo(x, y) {
    return x + y + z
  }
}

以上面程式碼來說， addTwo 使用到了 z 這個外部的變數，也就是 addAnother scope 的變數， 那這樣 addTwo 算 pure function 嗎？因為它依賴到自己 scope 以外的變數了對吧？

其實還是算，所以 input 也可以是自身 scope 以外的，只是你要確保它「不會變動」，在後續提到 Closure 的章節會再針對這個例外進行詳細的解釋。

no side effect 的好處、其他 side effects

no side-effects 的好處在哪裡呢？在於閱讀 code 的人腦袋運作的壓力變小了，如果有段程式碼直接依賴外部變數、mutate 外部狀態的 function，或有其他 side effect 時，閱讀時我們就必須時時追蹤變數值的變化，除了可讀性較不好以外，程式也很可能產生非預期的錯誤，難以追蹤目前狀態的變化。

但除了上述程式碼的範例以外，還有什麼會造成 side effect 呢？我們可以看看下圖：

看了上圖會發現，靠北，這不就是我們平常會做的事情嗎？如果不要 side effect 的話是要我怎麼活？

side effect 無所不在，不如說程式碼有 side effect 才是很正常的事情，所以 functional programming 並沒有在追求「no side effects」，而是「具有 side effect」（impure）和「沒有 side effect」(pure) 的程式碼要有明顯的分隔。

如同 Kyle Simpson 在課程裡說到的：

No such thing as “no side effects”, Avoid them where possible, make them obvious otherwise.

又或者是前輩良葛格在 這篇文 所說的：

FP 要追求的，其實不是整個程式都是 Pure，而是 Pure 與 Impure 有明顯的界線。

no side effect 不是最終要追求的目標，而是將 pure function 當成程式中的核心，side effect 則是像包裹在核心之外的殼，當發生預期外的事情時，我們就能更快速、有效的定位問題在哪。

Same input, Same output

「Same input, Same output」的概念很單純，就是你給 function 相同的 input，它都會給你相對應同樣的 output。

A function is a special relationship between values: Each of its input values gives back exactly one output value.

換句話說，這只是兩個數值之間的關係：輸入及輸出。所以下圖就是個合法的 function：

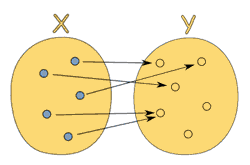
(此圖取自 mostly-adequate-guide)

從圖中可以看到，當你給他相同的 x 時，就可以得到相對應的 y，符合剛剛提及的 same input, same output 的概念。

如果是下圖就不是個合法的 function：

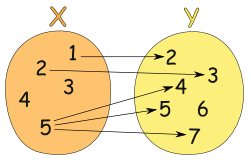
當你 x 給相同的 5 時，卻可能得到 4 或 5 或 7 三種不同的 y，代表這個結果是無法預期的，你每次給相同的值沒辦法保證它會得到一樣的結果，這就不是個 pure function。

以 Pure function 的特性來說，我們可以用不同的角度來看待 same input, same output 這件事，比如我們可以把它看成一張表：

又或者是看成 mapping ：

var isPrime = {
  1: false,
  2: true,
  3: true,
  4: false,
  5: true,
  6: false,
};

isPrime[3];
//=> true

我們有個 isPrime 的 mapping，key 代表 input，value 代表 output，當給入相對應的 key 時，就會得到相對應的 value，所以給入 3 的時候，因為 3 是質數，就會得到 true；如果給入 4 ，因為 4 不是質數，就會得到 false。

題外話，如果給入「江」呢？會得到什麼？true，因為江是質數，江直樹。

mapping 這個舉例，就是要說明當我們給 pure function. 相同的 input 時，就一定會得到相對應的 output。

Referential Transparency

前面提了「same input, same output」、「no side effects」，這兩個定義也是大多數 FP 文章講解 pure function 時會提到的兩個定義。

但還有比較少數的文章，會提到另一個重點，就是 pure function 是「Referential Transparency」的，這也是 Functional Light JS 的講者 Kyle Simpson 特別強調的一點，他認為最「full, cononical, complete」的 pure function 的定義，就是這個 function 是 referential transparency 的。

所以什麼叫 referential transparency？「可以用 return value 取代 function call，而整體的程式行為不會改變」，這個定義就叫做「Referencial Transparency」。

Referencial transparency means a function call can be replaced with it’s return value and not affect any of rest of the program.

所以舉例來說：

function add(x, y, z) {
    return x + y + z
}

add(1, 2, 3) // 6

如果在程式的某處，我用 6 取代 add(1, 2, 3) ，程式行為依舊不變，天下太平的話，這就叫 referencial transparency，也代表 add 是個 pure function。

那 referencial transparency 的好處是什麼呢？

在 Haskell 裡面，function 永遠是 pure，也就是永遠都會有 referencial transparency，compiler 可以基於這個特性，達到 memoize 每個東西的優點，因為他們可以把 return value 取代 function call 。

但 JavaScript 沒有，JavaScript 裡不會每個 function 都是 pure function，compiler 也不會幫你處理這些事情，那這樣來說，referencial transparency 在 JavaScript 的好處是什麼呢？答案是對 reader 的友善度，當 reader 重複閱讀到一樣的 function call 的時候，其實他不需要透過腦袋再思考一次，就能預測這段程式碼的結果，等同在腦袋進行 memoize 的事情，進而釋放部分腦袋的壓力，把專注力放在程式碼中其他更重要的事情。

Exercise - Extracting Impurity、Containing Impurity

Extracting Impurity

這邊指的是抽取出 impure 程式碼的技巧。

addComment 這個 function 是 impure function，可以看到它呼叫了 uniqueID 這個 function，以及 appendChild 操作了 DOM，顯而易見的都是屬於 side effect。

FP 講求的不是沒有 side effect，而是把 pure 和 impure 分出明顯的界線，因此我們可以改成這樣：

此時的 addComment 變得 pure，單純只是產生物件以及 DOM element 的 function，而 impure 的操作被放到了 function 外面，避免污染 pure function，因此分出了明顯的界線，抽取出了不純的地方。

但這方法不是每次都行得通，只是其中一個可行的辦法。

Containing Impurity

有時候沒辦法將 impure 的程式碼抽取出來，這時我們的辦法就是減少 impure 程式碼產生的範圍。

舉例來說，假設今天有一個來自第三方套件的 API：

我們可以確定第三方 API 會產生 side effect，因此做法是減少 side effect 的 surface，辦法是複製一份 numbers 的 array：

這樣無論怎麼操作，至少我們發生的 side effect 都是限縮在 line 9 - line 22 ，減少了 side effect 發生的範圍。

Adapters

但如果沒有辦法把 insertSortedDesc 包裹在 getSortedNums 裡呢？我們還可以怎麼做，Kyle Simpson 提供了第三種解法：

這邊透過六個步驟來處理 side effect：

1. 取得初始的 global value
2. 設定 numbers 的 initial value
3. side effect 的操作，就是操作 global state
4. capture the new value
5. restore the previous state
6. return the new value

雖然運作來說我懂在幹嘛，但概念上我可能還沒抓到真正的精髓，就先當作筆記放著 QQ

小結

pure function 在 FP 裡面至關重要，正因為 function 是 pure 的，我們才能享受到使用 FP 的好處，才可以運用到數學上的特性。

Kyle Simpson 在課程中提到，他認為「pure function」不是一個二元的概念，也就是說不是 0 和 1，只能分成「pure」和「impure」，而是類似於一個光譜，指的是「一個 function pure 的程度是多少」，function pure 的程度代表了 「level of confidence」，當你的 function 越 pure，你對這段程式碼的信心就越高，因為你更確定它的結果能夠預測，不會發生非預期的狀況搞你。

「pure function 不是二分法，pure 指的是程度上的差別」這說法，我也只有從 Kyle Simpson 的課程裡聽到， Kyle Simpson 算是在程式開發蠻有個人想法的人，所以課程中很多定義、說法可能都是他個人的理解，可以當作參考就好囉。

不過「same input, same output」、「no side-effects」、「referencial transparency」則是多數提及 pure function 一定會講到的定義，想知道更多的話可以點擊下方參考資料的連結。

最後，如果內容有錯誤的話也麻煩不吝指教，我會很感激的！

References

• Functional Programming Patterns With RamdaJS!

• Functional-Light JavaScript, v3

• 純粹的好，Pure Function 知道

• What Is a Pure Function in JavaScript?

• mostly-adequate-guide